Écoulement de solutions de polymères en milieux poreux : impact des effets viscoélastiques à l’échelle du pore sur les propriétés effectives à l´échelle de Darcy

Résumé : 

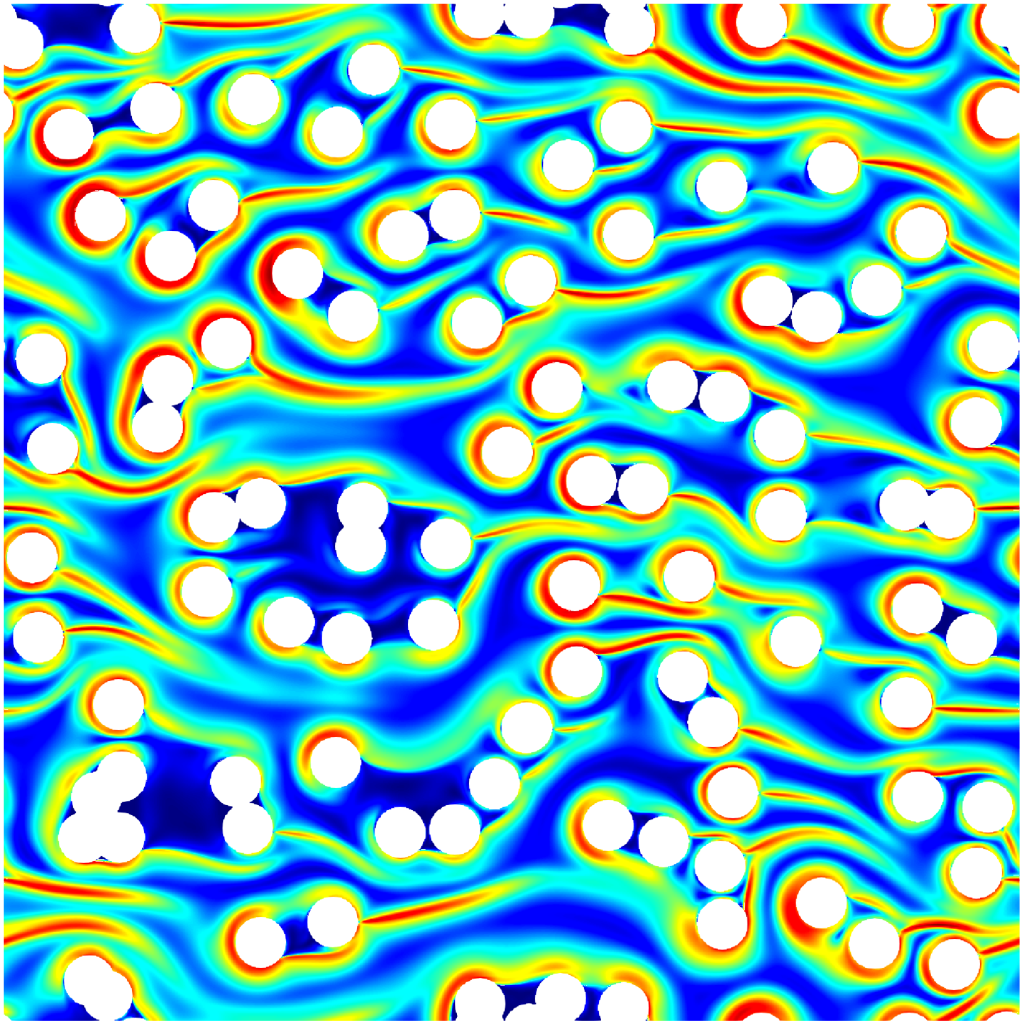
L’écoulement de solutions de polymères à travers des milieux poreux est un problème riche en mécanique des fluides qui combine la complexité des écoulements à travers des structures poreuses à celle de la rhéologie non linéaire du fluide. De tels écoulements peuvent présenter des comportements particuliers sur une large gamme d’échelles. Malgré des efforts continus, une compréhension claire des mécanismes à petite échelle impliqués et de leur lien avec les phénomènes à plus grande échelle fait toujours défaut. Dans ce travail, notre objectif est d’étudier certains des phénomènes physiques à l’échelle des pores et de les relier aux propriétés à l’échelle de Darcy. Pour ce faire, nous avons simulé l’écoulement de fluides viscoélastiques à travers des milieux poreux modèles, tels que des réseaux de cylindres en 2D ou des empilements de sphères en 3D, en résolvant, par des méthodes haute performance les modèles Oldroyd-B, FENE-P et FENE-CR. Dans la première partie, nous présentons donc un nouveau schéma de projection à grille décalée pour les écoulements viscoélastiques, ainsi que sa validation dans les cas de la cavité entraînée et de l’écoulement autour d’un cylindre confiné. Nous montrons ainsi que ce schéma possède une semi-différenciation spatiale cohérente avec une estimation de l’énergie libre, maintient la positivité du tenseur de conformation, est bien adapté au calcul haute performance (HPC), montre une bonne précision et peut être facilement utilisé pour une variété de lois constitutives viscoélastiques. Dans la deuxième partie, nous utilisons cette approche numérique pour montrer que les zones localisées de grande contrainte polymérique, appelées brins biréfringents, pilotent l’écoulement d’un fluide Oldroyd-B à travers des réseaux de cylindres en 2D. Nous constatons que ces brins génèrent en effet une réorganisation complète de l’écoulement avec une augmentation des zones de stagnation, un renforcement des chemins préférentiels et une division des canaux d’écoulement. De plus, nous montrons que cette réorganisation génère une augmentation de la dissipation visqueuse du solvant et que l’étirement des molécules de polymère dans les brins est associé à une production d’entropie. Ces deux phénomènes conduisent ainsi à une augmentation globale de la dissipation qui peut être directement liée à l’augmentation de la résistance à l’écoulement. Dans la troisième partie, nous étudions l’écoulement à travers un réseau hexagonal 2D de cylindres pour large une gamme de nombres de Weissenberg et différentes orientations du terme de forçage qui génère l’écoulement. Nous montrons que les brins biréfringents contrôlent la direction de l’écoulement moyen. Ces brins ont également tendance à adhérer aux cylindres voisins, ce qui conduit à des directions d’écoulement privilégiées et à une succession de bifurcations lorsque l’on fait varier l’angle du terme de forçage. L’effet le plus marquant est la présence d’une tristabilité associée à une hystérésis sur l’angle. Nous démontrons en outre que l’apparition d’un écoulement instationnaire est associée au mouvement des différents brins du réseau qui ouvrent et referment successivement les canaux d’écoulement. Ceci fournit une nouvelle perspective sur les écoulements viscoélastiques instationnaires à travers les milieux poreux et peut aider à comprendre la transition vers le chaos. Dans la quatrième partie, nous dérivons une forme moyennée du modèle Oldroyd-B à l’échelle de Darcy. Pour ce faire, nous utilisons une forme de linéarisation du problème, en considérant une limite très diluée, et nous décomposons le problème initial en une séquence de problèmes à différents ordres. Cette limite est très différente de la limite du faible nombre de Weissenberg car elle peut capturer la formation de brins biréfringents. Nous procédons à la moyenne spatiale de chaque problème et dérivons le modèle moyen correspondant pour obtenir une forme modifiée de la loi de Darcy. Les écoulements viscoélastiques en 2D dans des réseaux de cylindres ont suscité beaucoup d’intérêt, en particulier dans une série de travaux expérimentaux très récents, et nous ont aidés à comprendre les aspects fondamentaux de ces écoulements. Cependant, les écoulements à travers des structures 2D et 3D sont fondamentalement différents. Dans la dernière partie de ce travail, nous présentons donc des résultats préliminaires pour les écoulements viscoélastiques à travers des empilements 3D de sphères. De telles structures conduisent à des régions localisées de contrainte qui peuvent être considérées comme des brins 1D et des hyperplans 2D. Cela soulève donc des questions importantes sur la façon dont les écoulements viscoélastiques sont affectés par la dimensionnalité.