Simulations numériques de la condensation de gouttes
On donne ici un aperçu rapide des résultats obtenus récemment dans le cadre du projet sur la partie concernant la condensation de gouttes en considérant des configurations simplifiées. Les simulations effectuées on été réalisées avec le code de calcul DIVA (Dynamique Interfaciale pour la Vaporisation et l’Atomisation) développé à l’IMFT depuis 2009.
Étude préliminaire : simulation axisymétrique de la condensation d’une goutte d’eau statique dans un milieu sous-refroidi de dimension infinie
Afin de tester les capacités du code à simuler la condensation d’une goutte d’eau, des études préliminaires ont été effectuées. On a analysé la condensation d’une goutte d’eau statique, dont rayon initial est R0 0.01m, à la température de saturation pour un pression p=105 Pa, Tsat=373.15 K, immergée dans la phase vapeur correspondante sous-refroidie à la température T=353.15 K. Dans ces simulations le nombre de Jakob, Ja, est défini comme :
Ja = \frac{Cp (T_{sat}-T)}{L_v}
Le domaine de calcul est axisymétrique et il est montré sur la figure suivante.
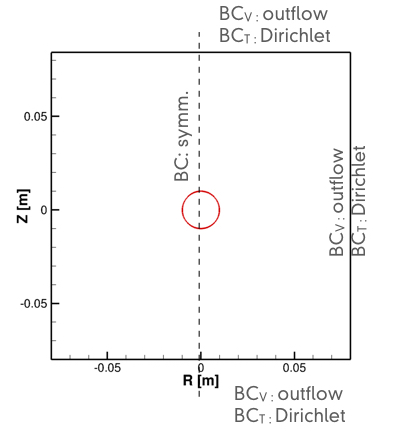
Dans cette configuration simplifiée, les résultats des simulations pourront être comparés à la solution théorique permettant de prédire l’évolution temporelle du rayon d’une goutte en condensation. Cette comparaison est tracée sur la Fig. 2 qui montre un très bon accord entre la simulation numérique et la loi analytique.
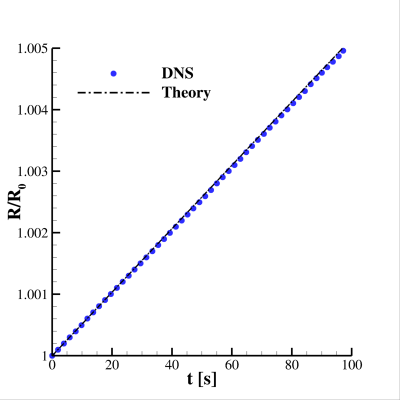
Cette comparaison a été faite une fois vérifie la convergence spatiale des simulations, obtenue avec une dimension de la cellule de calcul de 1.54×10-4m afin d’avoir 64 cellules dans le rayon de la goutte. Le champ de vitesse, qui montre une aspiration de la vapeur dans la goutte, et le champ de température sont illustrées sur les figures suivantes.
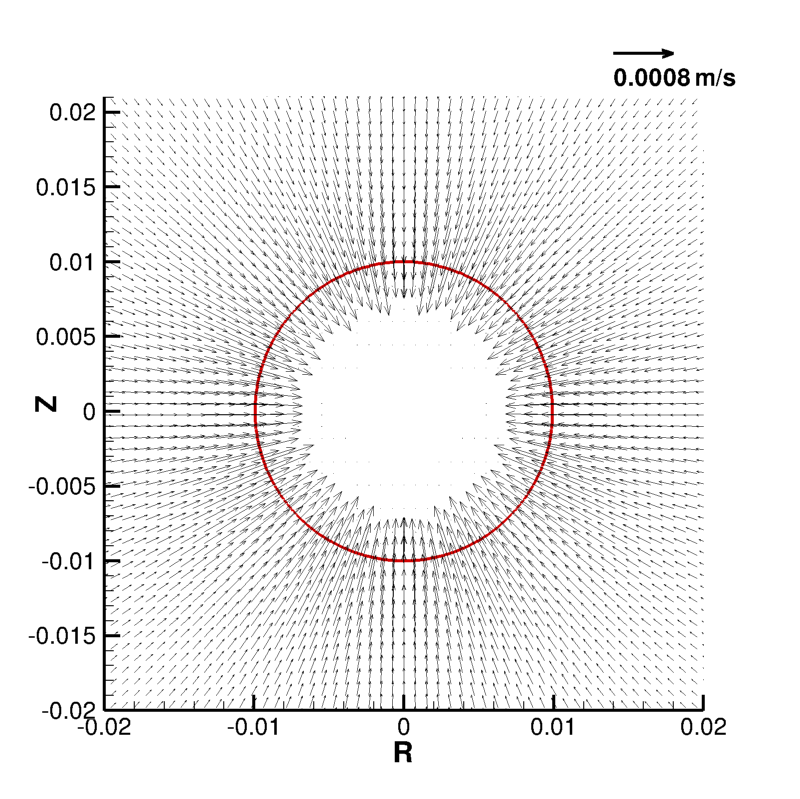
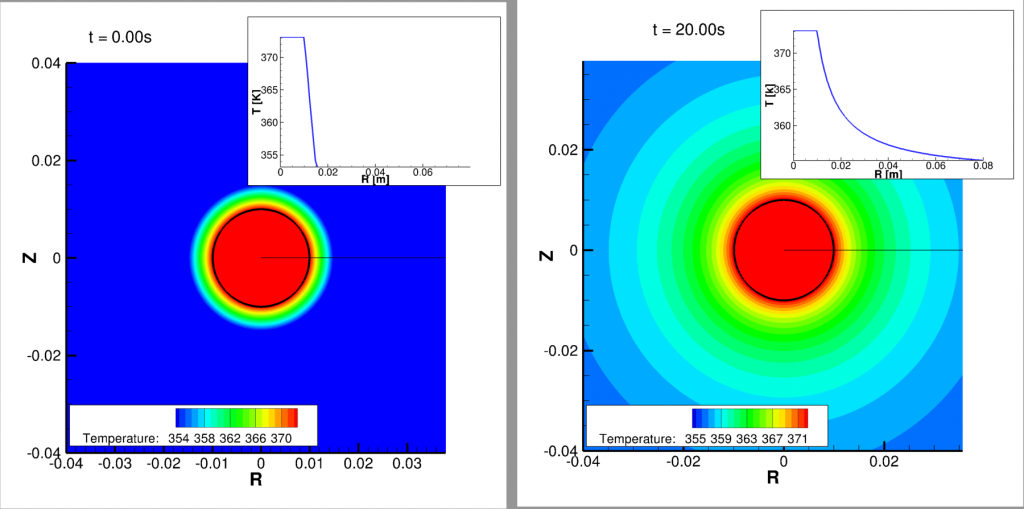
Simulations axisymétriques de la condensation d’une goutte posée sur une paroi solide isotherme
On présente l’étude de la condensation d’une gouttelette d’eau posée sur une paroi solide isotherme et immergée dans la phase vapeur correspondante. Cette analyse a été effectuée avec des simulations axisymétrique. La gouttelette et la parois sont à Tsat=373.15 K et la vapeur est sous-refroidie à T = 353.15k. La gouttelette a un rayon initial R0=0.002m. Les conditions aux limites choisies et le champ de température initial sont illustrés sur la Fig. 5.
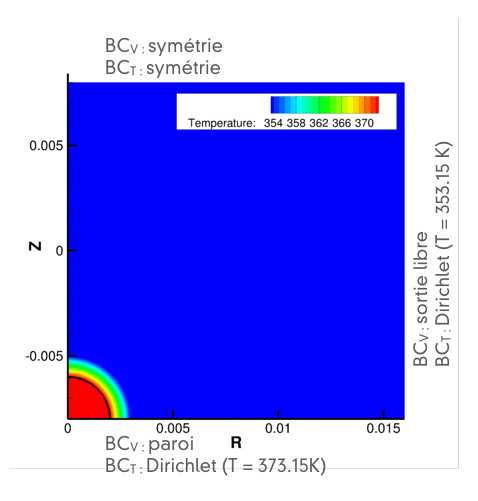
Une étude de convergence en espace sur la variation temporelle du volume de la goutte et sur le flux de chaleur échangé par la goutte et le champ de vapeur a montré que la convergence est satisfaite à partir d’une taille de la cellule de calcul égale à 3.125×10-5m, donc 64 cellules dans le rayon de la goutte.
Bien que le phénomène de condensation soit dépendant de plusieurs autres nombres
adimensionnels, l’influence du nombre de Jakob est prépondérante. C’est pourquoi nous proposons ici une étude paramétrique sur l’influence de ce nombre adimensionnel sur le flux thermique échangé par la goutte avec la vapeur ainsi que sur l’évolution temporelle du rayon de la goutte. Des simulations ont été réalisées pour une large gamme de nombres de Jakob, Ja = [0.01, 0.02, 0.4, 0.8, 1.25, 1.8].
Le champ de température et le champ de vitesse pour des différentes Ja sont visualisés sur le figures suivantes.
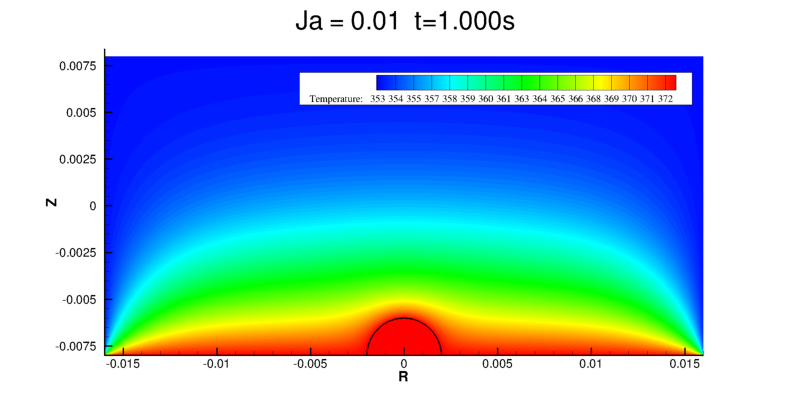
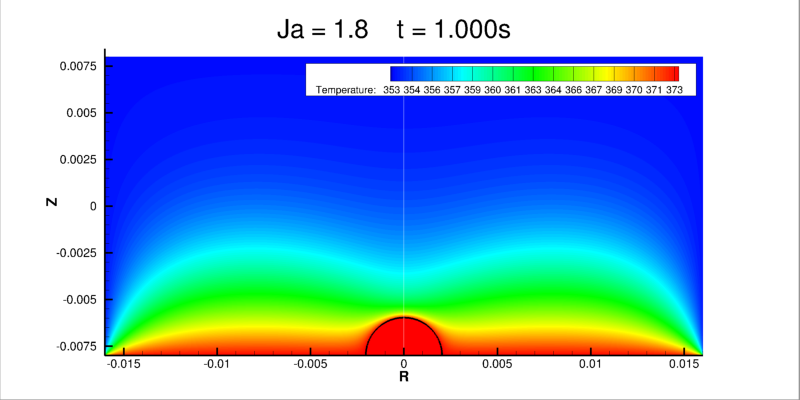
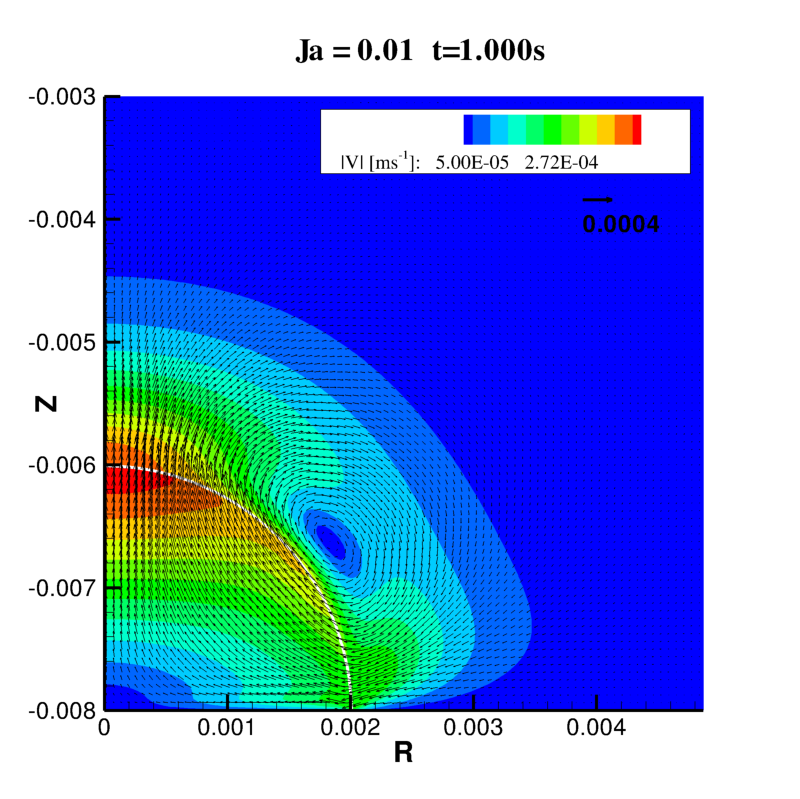
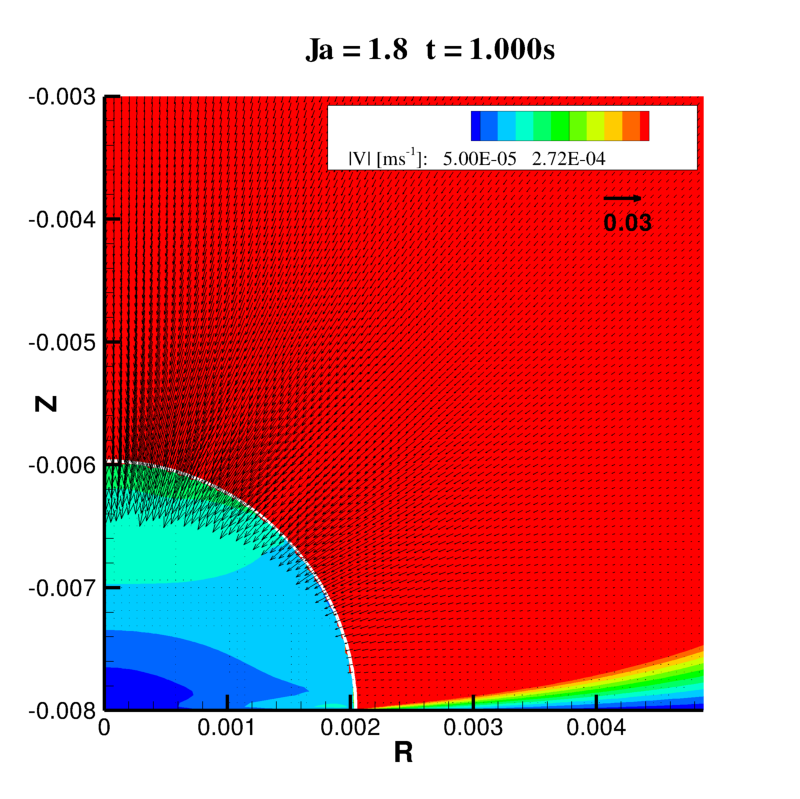
Le champ de température varie peu pour les valeurs de Ja faibles et, en effet, l’aspiration induit par la condensation est amplifiée lorsque le nombre de Jakob augment. Il en résulte que la couche limite thermique autour de la gouttelette s’affine pour les Ja plus élevés qui correspondent à une augmentation du taux de condensation.
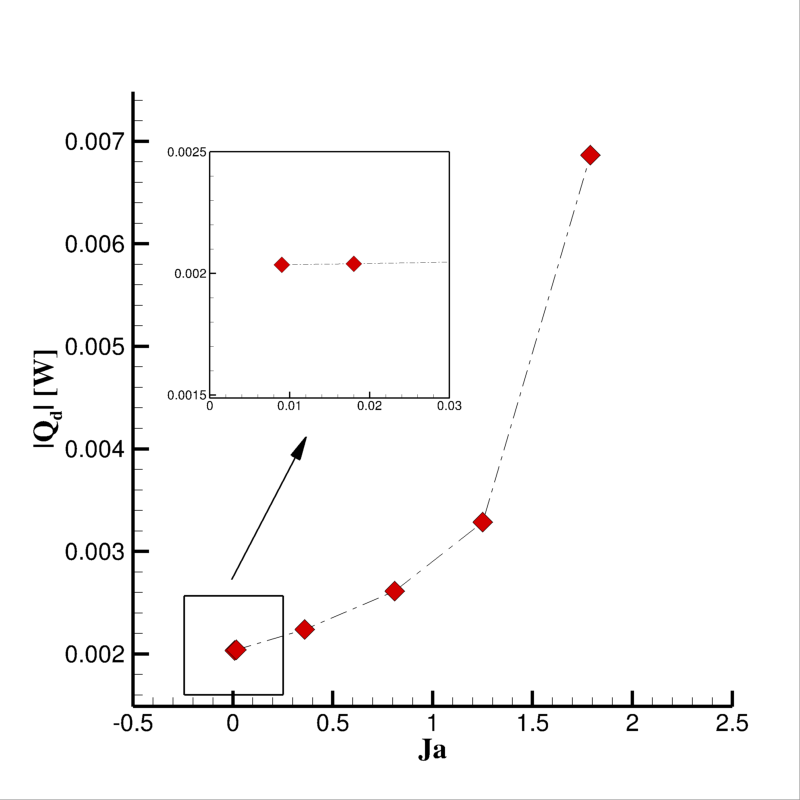
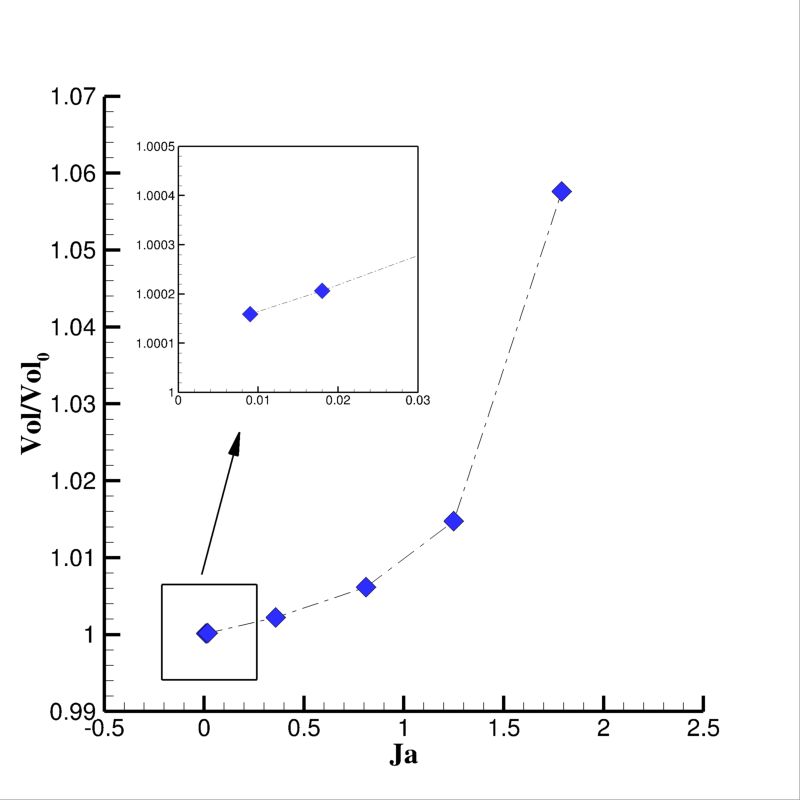
Pour les faible Ja on observe un phénomène de saturation (les deux points correspondent à Ja = 0.01 et Ja = 0.02 sur les Figs. 10 et 11 sont presque superposés), c’est-à-dire le flux thermique échangé ne dépend pas du nombre de Jakob. Ceci peut s’expliquer en supposant que dans cette configuration, le débit de condensation est trop faible pour générer un écoulement significatif aspirant la vapeur vers la goutte. Il en résulte que le flux échangé entre la goutte et la vapeur dépend uniquement de la conduction thermique autour de la goutte. En revanche, en augmentant le nombre de Jakob, l’intensité du champ de vitesse radiale qui en résulte modifie de façon significative le flux conductif que la goutte échange avec l’extérieur et donc le taux de condensation. On peut le constater sur les figures 10 et 11 que lorsque le nombre de Jakob est élevé les effets convectifs induits par la condensation deviennent significatifs et induisent une forte augmentation (non linéaire) du taux de condensation.
Simulations 3D de l’interaction entre une goutte en condensation posée sur une paroi isotherme et un écoulement de vapeur sous-refroidi
On présente ici les premières simulations tridimensionnelles de l’interaction entre une goutte en condensation posée sur une paroi, les deux étant à la température de saturation, Tsat=373.15K, et un écoulement laminaire de vapeur sous-refroidie. A notre connaissance, il n’existe à l’heure actuelle aucune étude permettant de calculer l’évolution du taux de condensation et du flux échangé entre une goutte et un écoulement externe dans ce type de configurations. La simulation numérique directe apparaît donc comme un outil de choix pour y parvenir, d’autant plus qu’elle permettra d’envisager par la suite des configurations encore bien plus complexes (plusieurs gouttes, gouttes déformées, coalescence et transition vers la formation d’un film liquide, écoulement turbulent) que celle présentées ici. L’écoulement de vapeur a été initialisé en résolvant les équations de Prandtl pour le champ de vitesse et pour le champ de température. Puisque le nombre de Prandtl qui caractérise notre
problème est proche de 1, les couches limites dynamique et thermique ont la même épaisseur (δv=δT), qui a été choisi, dans un premier temps, égal au rayon initial de la gouttelette, R0=0.002 m. Le nombre de Reynolds basé sur l’épaisseur de la couche limite a été choisi égal à RexL=100 qui correspond dans notre cas à une vitesse U∞=0.5 ms-1. Le domaine de calcul est illustré sur la Fig. 12.
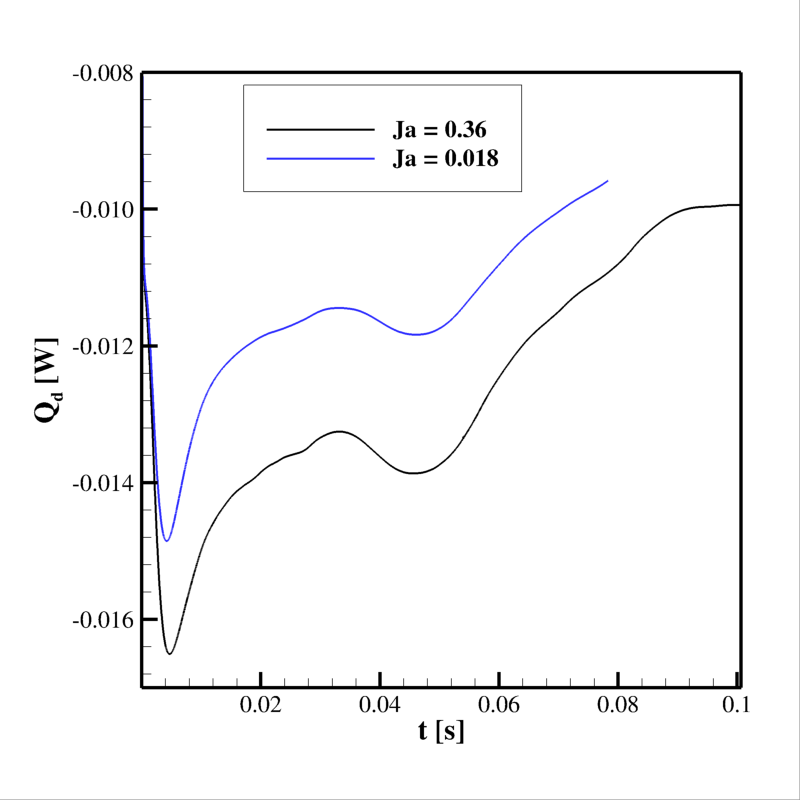
Une étude s’intéressant à l’influence de l’épaisseur de la couche limite par rapport au rayon de la goutte a également été initiée récemment, en considérant toujours pour un même nombre de Reynolds d’injection RexL=100. Le champ de température et les lignes de courant sont représentés sur les Figs. 15 et 16 pour deux valeurs différentes du rapport entre l’épaisseur de la couche limite et le rayon de la goutte, δ/R0=2 et δ/R0=4.
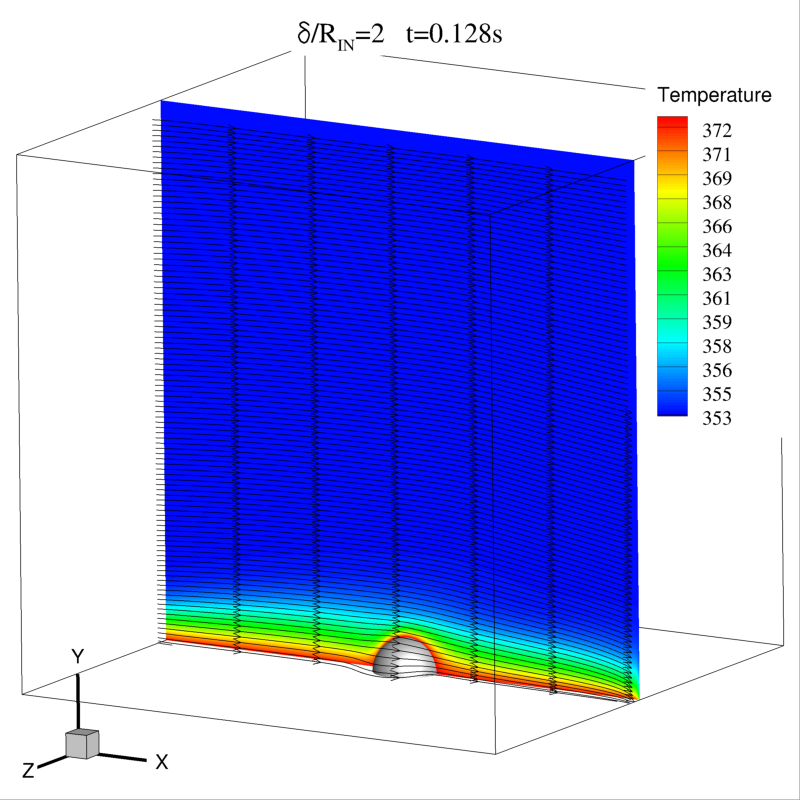
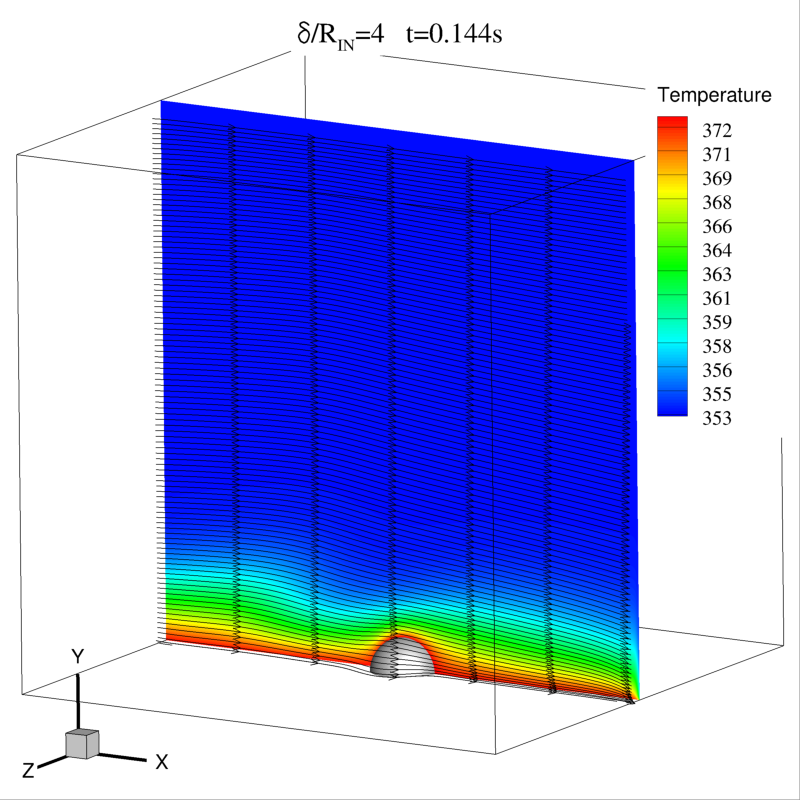
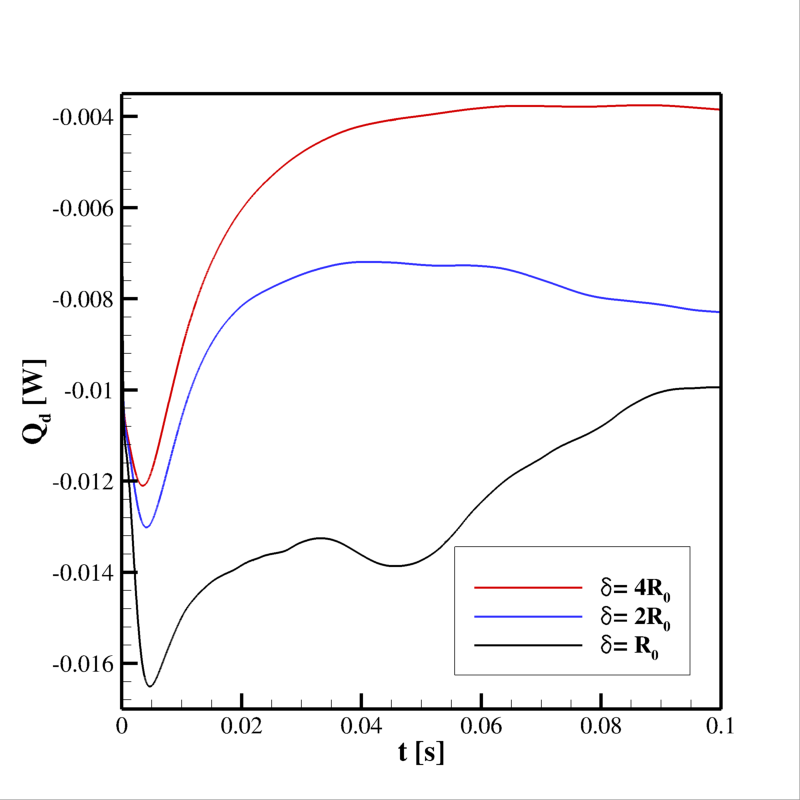
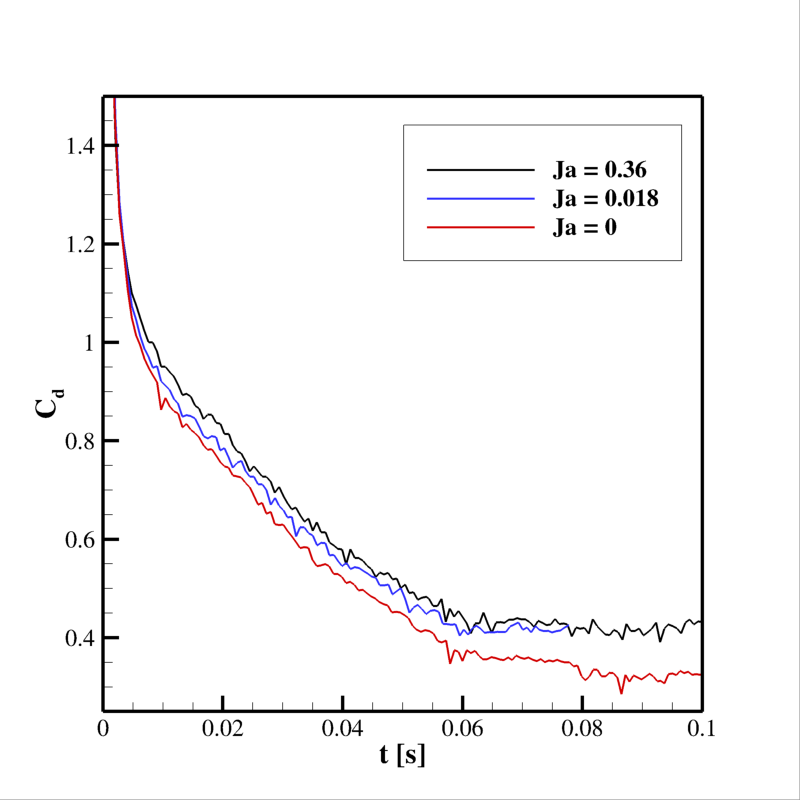
Les différences qualitatives observées entre les deux champs de température des Fig. 15 et 16 ont une conséquence sur le flux thermique instantané que la goutte échange avec le champ externe, comme on peut le voir sur la Fig. 17.





