Méthodes numériques pour la simulation numérique directe d’interfaces déformables
Le développement de méthodes numériques pour la simulation numérique directe d’écoulements diphasiques pour lesquels des déformations et/ou des topologies d’interface complexe doivent être prises en compte est une thématique importante développée dans l’équipe de recherche Interfaces, avec notamment une spécialisation sur la simulation de changement de phase liquide-vapeur ou solide-liquide. La réalisation de simulations dans des régimes impliquant un changement de phase liquide-vapeur en interaction avec une paroi surchauffée est notamment l’objet de nombreuses études.
Des outils et algorithmes de simulation récemment développés permettent de réaliser des simulations très résolues de gouttes en régime de Leidenfrost, c’est-à-dire de gouttes qui lévitent au-dessus d’une paroi surchauffée du fait de la contre-pression induite par l’évaporation intense survenant entre la goutte et la paroi surchauffée. Cela a été rendu possible par la combinaison de différents algorithmes de résolution permettant à la fois de résoudre à très petite échelle la fine couche de vapeur entre la goutte et la paroi surchauffée et de capturer la transition entre deux régimes de vaporisation de gouttes suivant la composition en espèces chimiques de la phase gazeuse environnante (mélange d’air et de vapeur d’eau ou vapeur d’eau saturée).
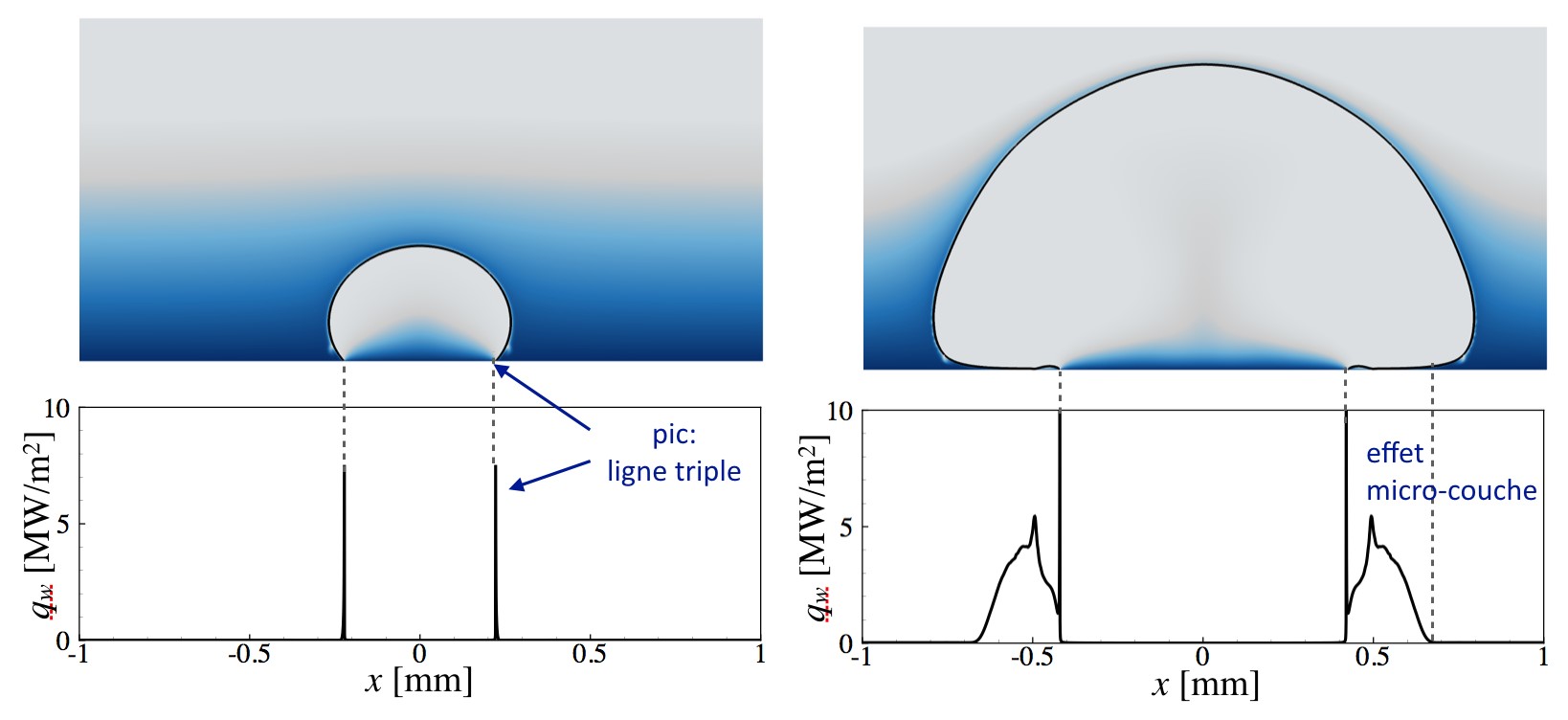
Une autre configuration impliquant un type de changement de phase liquide-vapeur différent, est également l’objet d’études approfondies, à savoir l’ébullition nucléée. Dans ce contexte, des études expérimentales récentes ont mis en évidence l’existence de deux régimes bien distincts, suivant qu’un film liquide fin, appelé microcouche, se développe ou pas, entre la paroi et la goutte en expansion. La transition entre ces deux régimes distincts, nommés respectivement ébullition en microcouche ou ébullition en ligne de contact, a été étudiée en réalisant des simulations numériques directes. Une étude paramétrique réalisée a notamment permis de définir une loi permettant de déterminer la frontière entre ces deux régimes dans l’espace des paramètres (essentiellement le nombre de Jakob, l’angle de contact et le nombre capillaire).