La pandémie de Covid 19 vue sous l’angle de la modélisation
C’est par pure curiosité scientifique que Patricia Cathalifaud, MDC Univ. Toulouse III-Paul Sabatier à l’IMFT, est passée ces temps derniers des écoulements de fluides à la modélisation de la pandémie de Covid 19.
Un peu comme si elle voyait la diffusion de la pandémie comme un écoulement, comme une vague.
Son défi personnel a débuté un mois environ avant le début du confinement national. Ce n’est guère surprenant pour cette scientifique régulièrement impliquée dans des recherches en mécanique des fluides en rapport avec la santé. Ses derniers travaux financés par l’ANR portent notamment sur la modélisation des mouvements liquidiens, ceux du sang et du liquide céphalo-rachidien, dans le cerveau humain et du singe marmouset.
Pour élaborer un modèle, elle s’est inspirée d’une publication transmise par son collègue Mokhtar Zagzoule, Pr Univ. Toulouse III-Paul Sabatier à l’IMFT : parue en 1987 dans la revue Nature, cette étude porte sur l’évolution de l’épidémie de VIH.
May R.M. & Anderson R.M. Transmission dynamics of HIV infection, Nature vol. 326 (12), 1987
Le modèle mis au point par Patricia intègre quant à lui 6 variables : personnes saines non porteuses, personnes infectées asymptomatiques, personnes infectées symptomatiques, personnes malades en réanimation, personnes décédées, personnes guéries immunisées. Il prend en compte seulement le facteur temps, le facteur géographique n’ayant pas été retenu. La logique mathématique sous-jacente est un système d’équations aux dérivées ordinaires fortement couplées les unes aux autres. En pratique, cela revient à faire passer les variables d’une catégorie à une autre, en jouant sur des taux et des durées de conversion entre les 6 variables. Les seules variations sont liées aux comportements humains et à ceux du virus.
Les données alimentant son modèle sont tirées au 15 février – jour de départ de la modélisation – de statistiques officielles issues du ministère de la santé et d’un site américain universitaire retraçant l’évolution mondiale de la maladie. Il est nécessaire de faire au départ quelques suppositions, comme le nombre de personnes asymptomatiques ou celui de personnes guéries, données non disponibles mi-février.
Au début, un léger décalage relatif aux cas symptomatiques apparaît entre les projections et les données officielles, mais le modèle se révèle rapidement performant pour prédire le nombre de malades graves, nécessitant des soins en réanimation, et le nombre de décès. Au fur et à mesure de la progression de l’épidémie, les prévisions issues de la modélisation sont de plus en plus proches du terrain, qu’elles concernent l’allure générale de la pandémie, son pic, ou sa régression. Le défi est donc relevé !
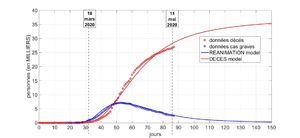
Le modèle montre même que la date du confinement a été particulièrement bien arrêtée : le sort de la France s’est joué à 4 ou 5 jours près ! La modélisation prédit aussi qu’en l’absence de confinement, le nombre de morts et de malades en réanimation aurait littéralement explosé, donc les mesures prises ont été particulièrement probantes. La prévision semble pencher vers un potentiel rebond, mais lent et relatif, en tablant sur le respect des mesures barrière après le déconfinement. L’élément incitant à la prudence est le comportement du virus, souvent énigmatique. En échangeant avec une ingénieure de recherche en biologie moléculaire, Patricia se voit confirmer la difficulté du décryptage de ce virus, risquant de prendre du temps.
A l’issue du déconfinement, que faire de cet outil ?
P. Cathalifaud songe à l’utiliser pour l’enseignement, autant au niveau des L1, pour une introduction à la modélisation dans le domaine du vivant, que des L3, M1 et M2, dans le cadre de projets. De petites vidéos pédagogiques sont prévues dans cette perspective dont une déjà publiée. Elle pense aussi à des stages pouvant donner lieu à publications. Cette prochaine responsable du master Mécanique du vivant à l’Université Toulouse III-Paul Sabatier est pleine de projets ! Une amélioration du modèle pourrait s’envisager en y ajoutant des méthodes d’estimation de paramètres de type filtre de Kalman (filtre de Kalman d’ensemble, par exemple), utilisés fréquemment dans les modèles de prédictions météorologiques.
En souhaitant que cet outil, si optimal soit-il, ne reprendra pas du service à l’occasion d’une seconde vague pandémique…





